Randomness, potato chips and the Law of Large Numbers.

Table of Contents

What are the chances!

Aren’t there times where things just feel almost too miraculous or improbable? Truly, the fact that you (or anyone else for that matter) are reading this blog post is a miracle to me, so thank you so much for spending some of your time here 😊.

You see, I also consider it somewhat of a miracle that I’m typing these words and equations today. Throughout secondary and tertiary education I detested math with a passion. There was nothing more meaningless to me than solving derivatives and calculating p-values. I just could not understand how the quadratic formula or that bell-shaped curve had anything to do with human existence. It was only through chance encounters with several instrumental mentors in university that I was exposed to probability theory, and I’ve grown to appreciate statistics ever since.

The purpose of this post is two-fold. Practically, this serves as a very concise guide to the fundamentals of statistics for readers who want some introductory content. Selfishly, I am writing this simply to share what caused my change of heart those years ago. My hope is that this post manages to either ignite or reignite your interest in statistics, while showing how reasoning with uncertainty can be both intuitive and fascinating.

One can always Expect Variance

There is no better place to start our discussion than \( X \). “What is \( X \)?”, you may ask. Well, \( X \) can be any observation you want! You could let \( X \) be the number of Lays potato chips in a large bag or the amount of water in the pacific ocean. What these two examples have in common is that they each have a defined set of possible events, with each event occurring with a specific probability (ranging from 0-1). For example, the probability that there is 1 chip is really close to 0, whereas the probability of having 70 chips might be close to 0.6.

And just like that we have defined the most important entity in statistics, the random variable \( X \), which can take possible values from a set \( \{ x_1, x_2, … \} \). When we assign a probability of occurrence \( \{ p_1, p_2, … \} \) to each value we define the probability distribution of \( X \):

\( P(X = x_i) = p_i \)

One important extension of the probability distribution, is that we can apply inequalities to the values that \( X \) might that. For instance, \( P(X \leq x_i) \) is simply the sum (or integral) of all the individual probabilities where \( X \) takes values less than or equal to \( x_i \).

Now coming back to the bag of chips, if we wanted to we could list all possible values of \( x_i \) and \( p_i \), but that would be incredibly tedious. Furthermore, it doesn’t really tell us anything about the overall properties of the bag of chips. This is where Expectation and Variance come into play. Formally, Expectation is defined as follows:

\( \mathrm{E}[X] = \sum_{i}^{} x_i \cdot p_i \)

One way to think about \( \mathrm{E}[X] \) is to view it as a sort of weighted sum, where each possible value of \(X\), is weighted by its corresponding probability of occurrence. \( \mathrm{E}[X] \) is also frequently referred to as the mean of a random variable and it is important to distinguish this from other instances where terms like “mean” and “average” are used (as we shall see later).

On a very related note, Variance is defined as follows:

\( \mathrm{Var}[X] = \mathrm{E}[(X - \mathrm{E}[X])^{2}] \)

Although often synonymous with the “spread” or “variability” of a particular phenomenon, \( \mathrm{Var}[X] \) can also be seen as a form of Expectation. More specifically, Variance is the expected squared deviation of a random variable from its own mean, or how much on average does a random variable deviate from its mean.

Lastly, if we were to get even more adventurous, we could even assume that the probability distribution of \( X \) follows a particular functional form that is defined by a set of parameters. More often than not, these values are symbolically referenced. For instance, we could say that \(X\) follows a Normal distribution \(X \sim \mathcal{N}(\mu ,\sigma^{2})\), that is parameterized by \( \mu = \mathrm{E}[X] \) and \( \sigma^{2} = \mathrm{Var}[X]\) .

An inquiry into the nature of potato chips

So far, we have encountered \( X \) and explored 2 of its most important properties, but dealing with 1 bag of chips at a time doesn’t make for very exciting statistics. Most of the time statistics concerns itself with the properties of \( N \) random variables \( X_{1}…X_{N} \), each of which (referred to arbitrarily as \( X_{i} \)) can be understood as entities that are sampled from an infinitely large sample space.

Suppose in a stroke of divine inspiration, you decide to investigate the potato chip mystery. You could then say to yourself:

“Okay, let \( X \) be the the number of potato chips in a large bag. Lets buy N=5 randomly chosen bags from 5 randomly chosen stores and see whats in them!”

Next, imagine that in all the excitement of data collection and chip eating, you decide to take this study one step further and repeat a N=5 sample the following week. Now if we examine the data from both samples (Fig 1), there are some important conclusions to be made. Generally, the samples do appear quite similar in their range of values and frequencies. Yet there are some differences, the repeated sample had 2 bags with 68 chips and did not have a bag with 70 chips.

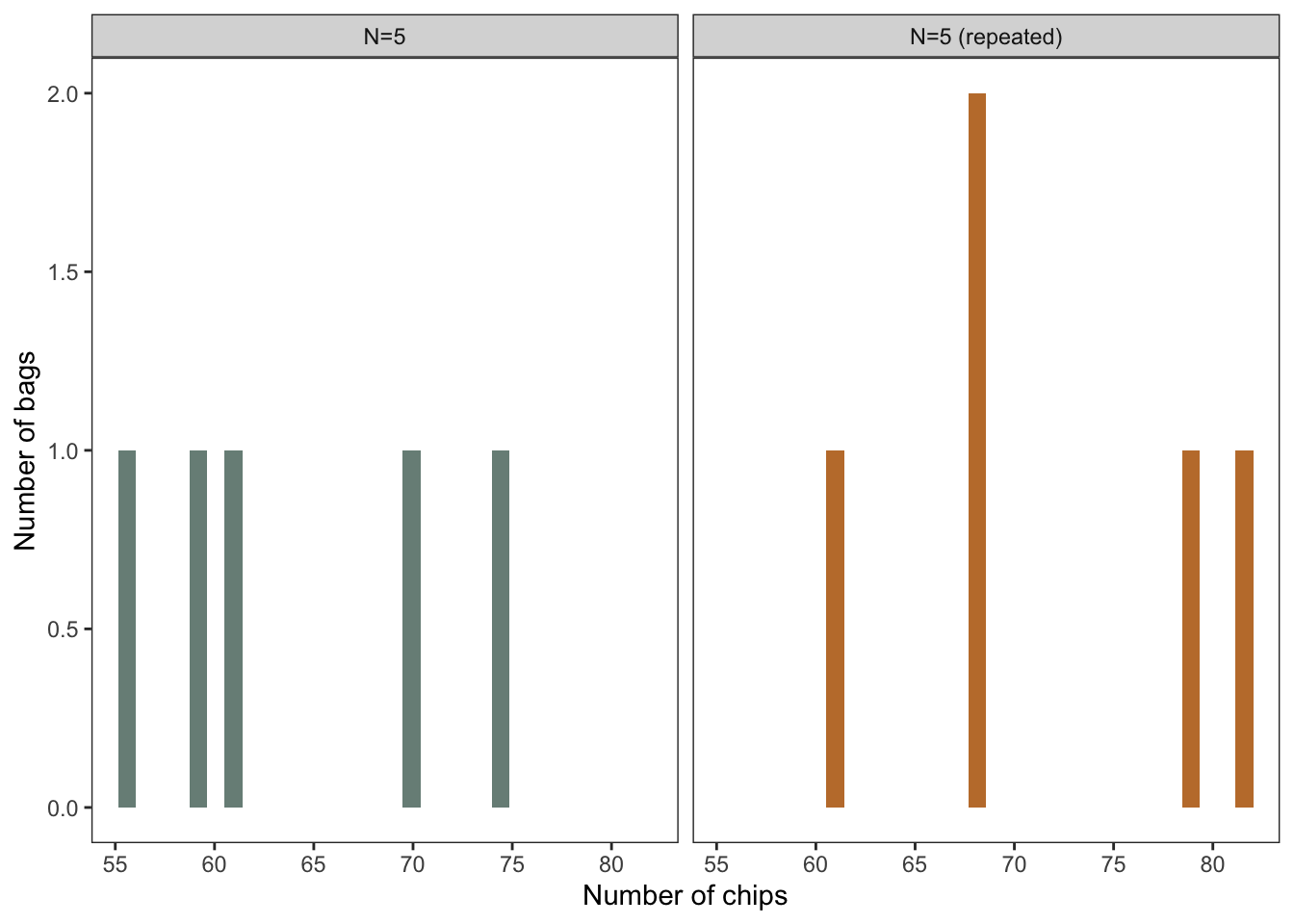
Figure 1: Two simulated random samples of potato chip count in five bags

Now armed with the knowledge of random variables, the difference between samples can be explained statistically. Even though we are able to obtain the realized values of each sample \( X_{1}…X_{N} \) bags, the number of chips in each bag \( X_{i} \) is a random variable and as such each sample of bags is fundamentally random!

Accordingly, we can calculate estimates from a sample while also treating the estimates like random variables. The most prolific of these estimates is none other than the Sample Mean \(\overline{X}\) :

\( \overline{X} = \frac{1}{N} \sum_{i=i}^{N} X_{i} \)

The sample means from the chip study were 64 and 71.6, and it would be quite likely that subsequent \(\overline{X}\) collected over several weeks would all be different. Since \(\overline{X}\) is a random variable just like \( X \), we can naturally also ask questions about its central tendency and variability. If we assume that each \( X_{i} \) bag in our sample has the same mean \( \mu \) and variance \(\sigma^{2} \), then :

\( \mathrm{E}[\overline{X}] = \mu \)

\( \mathrm{Var}[\overline{X}]= \frac{\sigma^{2}}{N} \)

The proof for these equations are neither particularly difficult nor relevant to this post but their results can still be easily understood. On average the sample mean will be equal to the true mean of \( X \) and the variance of the sample mean will equal the true variance of \( X \) scaled by the sample size.

This suggests that averaging out over many samples of \(\overline{X} \) gives us a definite value \( \mu \) and it does make intuitive sense that by increasing our sample size \(\overline{X} \) becomes less and less variable.

The Law of Large Numbers

Believe it or not, if you’ve made it this far into the post, you would have all the knowledge required to prove one of the most important theories in statistics, the Law of Large Numbers (LLN)! The LLN should be no stranger to most, but what is it really? For the sake of simplicity, we’ll generalize both the weak and strong versions of the LLN to :

\( \overline{X}_N \rightarrow \mu \; as \; N \rightarrow \infty \)

Earlier we mentioned that the expectation of the sample average of potato chips \( \mathrm{E}[\overline{X}] \) is equal to the true mean number of potato chips \( \mu \). Now with the LLN, we see that as the number of potato chips in our sample \( N \) gets larger and larger, the sample average \( \overline{X} \) itself converges to \( \mu \). Intuitively, if we see \( \overline{X} \) as an attempt to “approximate” \( \mu \) with our limited sample size \( N \), it makes sense that this approximation gets better as \( N \) increases. But enough talking, lets get to the proof, which is adapted from the amazing textbook Mathematical Statistics and Data Analysis.

The first (and most tedious) step is to prove Markov’s Inequality, which states that if \( X \) is a non-negative random variable then for any \( t > 0 \) :

\( P(X \geq t) \leq \frac{\mathrm{E}[X]}{t} \).

Earlier, since we defined \( \mathrm{E}[X] \) as a sum, we can split this sum for values of \( x_i \) that are less than or greater than \( t \):

\( \mathrm{E}[X] = \sum_{i: x_i < t}^{} x_i \cdot p_i + \sum_{i: x_i \geq t}^{} x_i \cdot p_i \)

Since \( X \) is non negative, \( \mathrm{E}[X] \) is always at least as large as one of its constituent parts. Furthermore, if we consider the second summation, its \( x_i \) values are all guaranteed to be at least as large as t. Lastly, after replacing \( x_i \) with \( t \) we can move \( t \) outside the summation and sum up all the \( p_i \) for \( x_i \geq t \), to give us:

\( \begin{aligned} \mathrm{E}[X] &\geq \sum_{i: x_i \geq t}^{} x_i \cdot p_i \\ &\geq \sum_{i: x_i \geq t}^{} t \cdot p_i \\ &= t.P(X \geq t) \end{aligned} \)

Shifting the terms around gets us Markov’s inequality, which implies that as the probability of \(X\) being much larger than \(E[X]\) gets smaller as the difference gets bigger (imagine substituting t = \(E[X]\), then values of t > \(E[X]\)).

With most of the hard work behind us, we can address Chebyshev’s Inequality. First, we define a new random variable \(Y = (X - \mu)^{2} \). If this looks familiar, its because it is, now conveniently having \(E[Y] = \sigma^{2}\). Next, we fit \(Y\) into Markov’s Inequality, letting \(\epsilon = t^{2}\) and taking the square root:

\( \begin{aligned} P(Y > \epsilon) &= P((X - \mu)^{2} > t) \\ &= P(|X - \mu| > t) \\ &\leq \frac{\sigma^{2}}{t^{2}} \end{aligned} \)

Finally with an equality involving \(|X - \mu|\), we can substitute \(X\) for \(\overline{X}\). Recalling our earlier definitions of \( \mathrm{E}[\overline{X}] \) and \( \mathrm{Var}[\overline{X}]\):

\( P(|X - \mu| > t) \leq \frac{\sigma^{2}}{N . \epsilon} \)

So we see that as \( N \) gets larger, the term on the right gets smaller and eventually goes to 0. What this means is that the as N goes to infinity, the probability that the absolute difference between \(\overline{X}\) and \(\mu\) is greater than any \(t\) (no matter how small), goes to 0. Loosely, \(\overline{X}\) just gets impossibly close but never reaching \(\mu\).

And that’s a wrap! A very brief introduction to statistics, a study on potato chips and the proof of a very important theorem. Once more, I hope that you were able to take away something from this post and perhaps see statistics in a different light.