1.1 An Introduction to Causal Inference
Attempting to solve a truly confounding problem.
Table of Contents
Why bother finding out why?
The first text on Causal Inference that I had the privilege of experiencing was Prof Judea Pearl’s Causality. Reading it as a graduate student, the novel graph theorems that Prof Pearl conceived of were unlike anything I ever encountered. As enriching (and confusing) as causal graph models were, I found the entire experience to be somewhat counter-intuitive. As conscious, intelligent life-forms, shouldn’t our understanding of cause and effect be second nature to us, with or without the usage of complex models? When water spills after a cup is knocked over or when a room door swings open after a strong gust of wind, cause and effect are established effortlessly. Why then do things get so much more complicated when we investigate whether the usage of paracetamol causes an increased risk of stroke?
Putting this question aside, it is of course no small coincidence that much of medical statistics is fundamentally concerned with causality. Does a particular treatment cause improved patient outcomes? Does geographical location cause lower life expectancy? Yet most observational hypotheses and findings are phrased very differently :
Our study finds an association / link between _ and _.
At risk of sounding unwittingly critical, this discrepancy between expectation and reality is an inevitable consequence of standard statistical theory. Try as we might, conventional statistical methods do not address causality. As such, a distinct set of tools are required to separate association from causation.
The elephant in the room
There is perhaps no phrase that is more overused and under-explained in statistics education than:
“Correlation does not imply Causation”
In the interest of time, this article will only focus on addressing what correlation is and is not, while only suggesting the existence of causal mechanisms. The following article in this series will then elaborate on a formal definition and framework for causal inference. Additionally, all content from this point will use fundamental statistical theorems involving random variables. For an introduction to statistical theory, feel free to check out this article.
I believe it is most helpful to begin by understanding correlation from the perspective of independence, which is a property that is shared between 2 or more random variables. Considering just and , we can first define their joint distribution as . For instance, we could arbitrarily say that the probability of both a thunderstorm () and solar eclipse () occurring tomorrow is 0.00001. and are independent if and only if their joint distributions can be factorized into the product of the respective marginal distributions:
Additionally, we can apply this independent factorization to the joint expectation of (proof omitted), giving :
Although this can seem slightly unintuitive, we can use this property of independence on the conditional distribution of . Following our earlier example, we could say that the probability of a thunderstorm given that a solar eclipse occurs tomorrow . Assuming that and are independent, the next few equations should bring back all too familiar memories of tertiary math lessons:
From the perspective of conditional probability, independence just means that information regarding of the outcome of either or has no effect on the probability distribution of the other (i.e conditional = marginal).
Next, relating independence to correlation. Correlation is defined as . The numerator of this expression is called the covariance of and , and correlation is just a scaled version of it. More importantly, we can define covariance as :
Although some algebraic manipulation was omitted, we can see that is actually just the expected “average” product of and ’s deviation from each of their own means. More importantly, if and are independent, then :
Ultimately, if and are independent they are uncorrelated with a correlation of 0. Here, it is very important to note that the converse statement is NOT true, i.e if and have a correlation of 0, it is possible that they are dependent. This is because correlation is only a measure of the linear relationship/dependence between and , but this is a story for another time.
At the end of the day we can definitively say that correlation between and simply implies that they are not independent. Or in other words, that and are dependent random variables that are associated with each other.
A study in Springfield
As the world emerges from the seemingly inescapable grasp of a pandemic, even the once tranquil hamlet of Springfield slowly recovers from the effects of Covid-19. As a newly registered medical student assigned to Springfield General Hospital, you are tasked to analyze an observational dataset on the long-term effects of a new antiviral drug on Covid-19 recovery. You find out that the Springfield dataset (Table 1) comprises of each patient’s name and 2 coded variables :
- : { C: treated with control, T: treated with antiviral }
- : { : persistent shortness of breath, : no shortness of breath }
| Patients | A | Y |
|---|---|---|
| Homer | C | 0 |
| Bart | T | 0 |
| Lisa | C | 1 |
| Millhouse | T | 0 |
| Krusty | T | 0 |
| Maggie | C | 1 |
| Marge | T | 1 |
| Ned | T | 0 |
| Apu | T | 0 |
| Mr Burns | T | 0 |
| Selma | C | 1 |
Given the dataset’s relatively simple structure, a cursory observation would be enough to reveal the presence of a relationship between the treatment and outcome . Using the aforementioned definitions of conditional probability, we could calculate the observed and . Since the marginal distribution of does not equal its conditional distribution, we can definitively conclude that there is a positive association between treatment and outcome . Accordingly, treatment and outcome are positively correlated with a correlation coefficient of 0.607.
With this analysis completed, a report is then made to the hospital with the conclusion that antiviral treatment results in improved long-term outcomes in Covid-19 patients.
By now, particularly astute readers might have noticed something curious about the data. So for the sake of demonstration, assume that an additional variable representing each patient’s gender was accidentally omitted from the final dataset. Additionally, assume that the true underlying causal structure of the data was actually as shown in (Fig 1), where a directed arrow means that G causes Y. As mentioned earlier, a formal definition of causation will be deferred to the next post, but it is sufficient to know that causation implies association, i.e if G causes Y, then G is associated with Y.
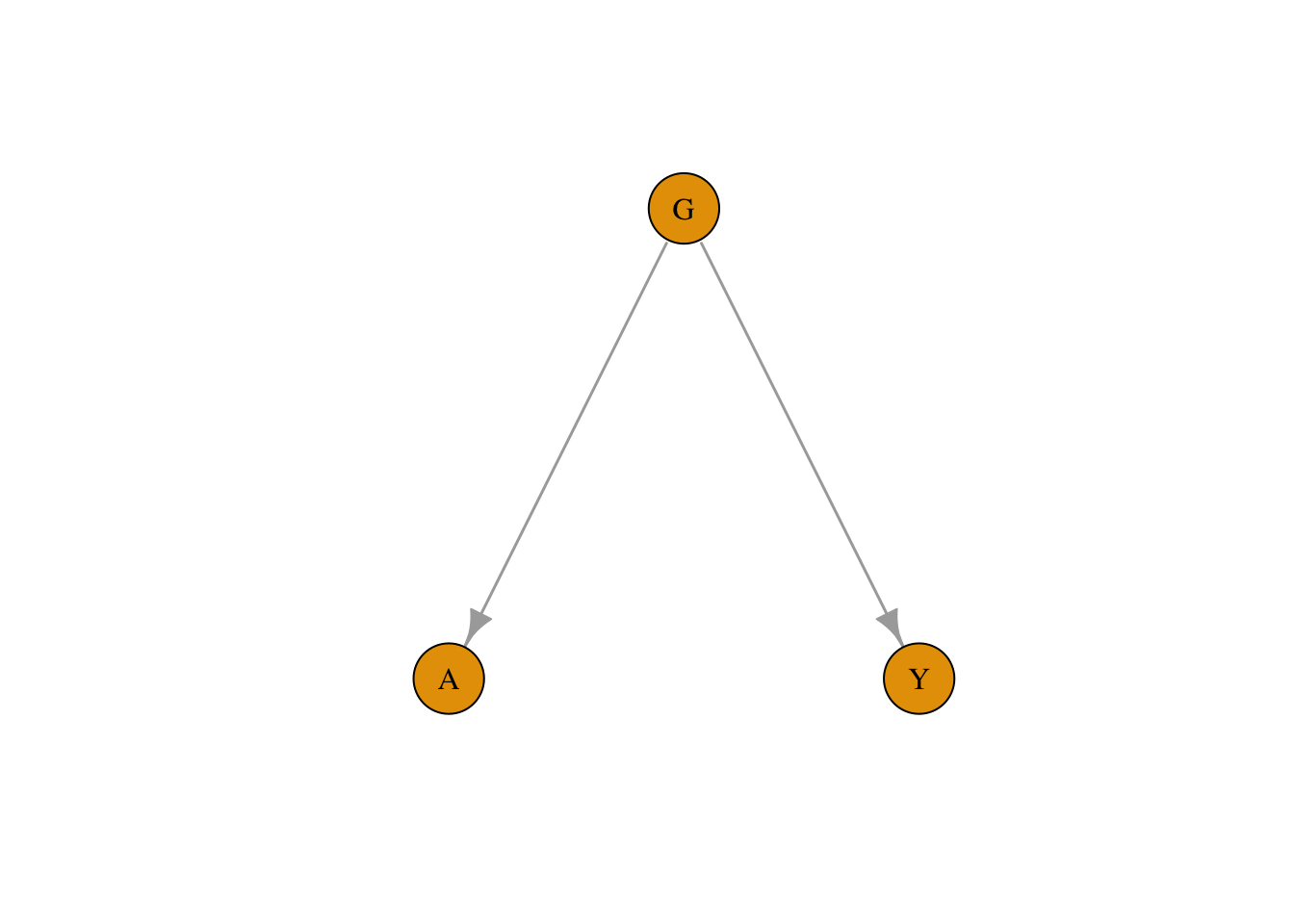
Figure 1: The underlying causal structure of the Springfield dataset
What is most notable about this is that the dataset was generated with no direct causal link between and . Which is to say, that antiviral treament has no causal effect (positive or negative) on long-term Covid-19 outcomes despite both variables being strongly correlated.
To delve deeper into why correlation truly does not imply causation, the full dataset is presented in (Table 2), with its rows sorted by gender . From this we can see that males were disproportionately assigned the antiviral and every male patient had a positive outcome. As a result, antiviral treatment became deceptively associated with positive outcomes.
Because is a common cause of both and it is also known as a confounding variable. The presence of confounds the true relationship between and , creating correlation even when there is no causal effect. And it is the presence of confounding variables that make the inference of causal effects in observational data so challenging.
| Patients | A | Y | G |
|---|---|---|---|
| Lisa | C | 1 | F |
| Maggie | C | 1 | F |
| Marge | T | 1 | F |
| Selma | C | 1 | F |
| Homer | C | 0 | M |
| Bart | T | 0 | M |
| Millhouse | T | 0 | M |
| Krusty | T | 0 | M |
| Ned | T | 0 | M |
| Apu | T | 0 | M |
| Mr Burns | T | 0 | M |
Before concluding this section, readers might fairly point out that the data presented in Table 2 could have also arisen if there was indeed a true causal relationship between . If so, how does one distinguish the presence of a true causal effect in the presence of confounding variables?
The answer to that question has become the life’s work of numerous professors and it is an answer I hope to get closer towards with each blog post. But for now, it will suffice to say that this dataset was generated purely for demonstrative purposes and lacks the sample size and quality for proper causal inference.
Heartfelt acknowledgements
So, where do we go from here? Well, the next post will introduce the Potential Outcomes framework, which will be the cornerstone for future discussions. Then, we will see that the search for causal effects isn’t actually that daunting. In fact you’ve probably done some causal inference as a student! After which, we will embark on an unforeseeably long journey exploring the various methods for causal inference in observational data.
Before ending this post, I would be remiss if I did not express my deepest gratitude to the teachers and mentors who made this learning journey possible:
I am extremely grateful to Prof Fan Li and Prof Linda Valeri for publishing their amazing course materials online. Their teachings play an instrumental role in structuring my understanding of causal inference.
The definitive textbooks by Prof Imbens & Prof Rubin, Prof Hernán & Prof Robins and Prof Vanderweele were (and still are) ever-present companions at every study session.
Lastly, for giving me my very first introduction to causal inference in a memorably warm and cordial job interview, I am very thankful to Prof Jonathan Huang.
